Febrero 16 de 2016
Veremos un poco del Sistema Binario,Sistema Decimal y Sistema Hexadecimal
Sistema binario
El sistema binario, llamado también sistema diádico1 en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los que se utilizan en las computadoras, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
Representación
En el sistema binario solo se necesitan dos cifras.
En informática, un número binario puede ser representado por cualquier secuencia de bits (dígitos binarios), que suelen representar cualquier mecanismo capaz de usar dos estados mutuamente excluyentes. Las siguientes secuencias de símbolos podrían ser interpretadas como el mismo valor numérico binario:
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| ¦ | − | ¦ | − | − | ¦ | ¦ | − | ¦ | ¦ |
| x | o | x | o | o | x | x | o | x | x |
| y | n | y | n | n | y | y | n | y | y |
El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En una computadora, los valores numéricos pueden representar dos voltajes diferentes; también pueden indicar polaridades magnéticas sobre un disco magnético. Un "positivo", "sí", o "sobre el estado" no es necesariamente el equivalente al valor numérico de uno; esto depende de la nomenclatura usada.
De acuerdo con la representación más habitual, que es usando números arábigos, los números binarios comúnmente son escritos usando los símbolos 0 y 1. Los números binarios se escriben a menudo con subíndices, prefijos o sufijos para indicar su base. Las notaciones siguientes son equivalentes:
- 100101 binario (declaración explícita de formato)
- 100101b (un sufijo que indica formato binario)
- 100101B (un sufijo que indica formato binario)
- bin 100101 (un prefijo que indica formato binario)
- 1001012 (un subíndice que indica base 2 (binaria) notación)
- %100101 (un prefijo que indica formato binario)
- 0b100101 (un prefijo que indica formato binario, común en lenguajes de programación)
Sistema de numeración decimal
El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras : cero (0) - uno (1) - dos (2) - tres (3) -cuatro (4) - cinco (5) - seis (6) - siete (7) - ocho (8) y nueve (9).
Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método del binario o el hexadecimal. Hay otros sistemas de numeración, como el romano, que es decimal pero no-posicional.
Escritura decimal
En el sistema de numeración posicional de base diez, los números que no son enteros, es decir, los números con parte fraccionaria tienen una representación en forma de número decimal. Sin contar las secuencias recurrentes de la forma 0,999…, la escritura es única y puede ser de dos tipos:1
Esta ley de tricotomía aparece en todo sistema de notación posicional en base entera n, e incluso se puede generalizar a bases irracionales, como la base áurea.
Así, las fracciones irreducibles cuyo denominador contiene factores primos que factorizan a 10 (2 y 5), tiene una representación finita. Si contienen factores primos distintos de aquellos que factorizan a 10, no tienen representación finita: la parte fraccionaria presentará un período de recurrencia pura cuando no haya ningún factor primo en común con la base, y recurrencia mixta (aquella en la que hay dígitos al comienzo que no forman parte del período) cuando haya al menos un factor primo en común con la base. Si contiene un desarrollo ilimitado no periódico, esta representación corresponde a un número irracional.
Sistema hexadecimal
El sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues loscomputadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 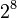 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 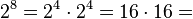
 , que equivale al número en base 16
, que equivale al número en base 16 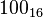 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.
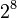 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 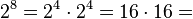
 , que equivale al número en base 16
, que equivale al número en base 16 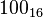 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.
En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:
Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956por la computadora Bendix G-15.
Decimal a binario
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Este será el número binario que buscamos.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Este será el número binario que buscamos.
- Ejemplo
- Transformar el número decimal 131 en binario. El método es muy simple:
131 dividido entre 2 da 65 y el residuo es igual a 1
65 dividido entre 2 da 32 y el residuo es igual a 1
32 dividido entre 2 da 16 y el residuo es igual a 0
16 dividido entre 2 da 8 y el residuo es igual a 0
8 dividido entre 2 da 4 y el residuo es igual a 0
4 dividido entre 2 da 2 y el residuo es igual a 0
2 dividido entre 2 da 1 y el residuo es igual a 0
1 dividido entre 2 da 0 y el residuo es igual a 1
-> Ordenamos los residuos, del último al primero: 10000011
En sistema binario, 131 se escribe 1000001.
Decimal (con decimales) a binario
Para transformar un número del sistema decimal al sistema binario:
- Se transforma la parte entera a binario. (Si la parte entera es 0 en binario será 0, si la parte entera es 1 en binario será 1, si la parte entera es 5 en binario será 101 y así sucesivamente).
- Se sigue con la parte fraccionaria, multiplicando cada número por 2. Si el resultado obtenido es mayor o igual a 1 se anota como un uno (1) binario. Si es menor que 1 se anota como un 0 binario. (Por ejemplo, al multiplicar 0.6 por 2 obtenemos como resultado 1.2 lo cual indica que nuestro resultado es un uno (1) en binario, solo se toma la parte decimal del resultado).
- Después de realizar cada multiplicación, se colocan los números obtenidos en el orden de su obtención.
- Algunos números se transforman en dígitos periódicos, por ejemplo: el 0.1.
- Ejemplo
0,3125 (decimal) => 0,0101 (binario).
Proceso:
0,3125 * 2 = 0,625 => 0
0,625 * 2 = 1,25 => 1
0,25 * 2 = 0,5 => 0
0,5 * 2 = 1 => 1
En orden: 0101 -> 0,0101 (binario)
Binario a decimal
Para realizar la conversión de binario a decimal, realice lo siguiente:
- Comience por el lado derecho del número en binario. Multiplique cada dígito por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 20).
- Después de realizar cada una de las multiplicaciones, súmelas todas y el número resultante será el equivalente al sistema decimal.
- Ejemplo
El número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:

entonces se suman los números 64, 16 y 2:
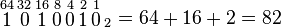
Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:

Binario a decimal (con parte fraccionaria binaria)
1. Inicie por el lado izquierdo (la primera cifra a la derecha de la coma), cada número deberá ser multiplicado por 2 elevado a la potencia consecutiva a la inversa (comenzando por la potencia -1, 2-1).
2. Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.
- Ejemplos
- 0,101001 (binario) = 0,640625(decimal). Proceso:
1 * 2 elevado a -1 = 0,5
0 * 2 elevado a -2 = 0
1 * 2 elevado a -3 = 0,125
0 * 2 elevado a -4 = 0
0 * 2 elevado a -5 = 0
1 * 2 elevado a -6 = 0,015625
La suma es: 0,640625
Binario a hexadecimal
Para realizar la conversión de binario a hexadecimal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
| Número en binario | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Número en hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.
- Ejemplos
- 110111010 (binario) = 1BA (hexadecimal). Proceso:
1010 = A
1011 = B
1 entonces agregue 0001 = 1
Agrupe de derecha a izquierda: 1BA
Hexadecimal a binario
Note que para pasar de Hexadecimal a binario, se remplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario.
Tabla de conversión entre decimal, binario, hexadecimal, octal, BCD, Exceso 3 y Gray o Reflejado
| Decimal | Binario | Hexadecimal | Octal | BCD | Exceso 3 | Gray o Reflejado |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 | 0000 | 0011 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 | 0100 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 | 0101 | 0011 |
| 3 | 0011 | 3 | 3 | 0011 | 0110 | 0010 |
| 4 | 0100 | 4 | 4 | 0100 | 0111 | 0110 |
| 5 | 0101 | 5 | 5 | 0101 | 1000 | 0111 |
| 6 | 0110 | 6 | 6 | 0110 | 1001 | 0101 |
| 7 | 0111 | 7 | 7 | 0111 | 1010 | 0100 |
| 8 | 1000 | 8 | 10 | 1000 | 1011 | 1100 |
| 9 | 1001 | 9 | 11 | 1001 | 1100 | 1101 |
| 10 | 1010 | A | 12 | 0001 0000 | 1111 | |
| 11 | 1011 | B | 13 | 0001 0001 | 1110 | |
| 12 | 1100 | C | 14 | 0001 0010 | 1010 | |
| 13 | 1101 | D | 15 | 0001 0011 | 1011 | |
| 14 | 1110 | E | 16 | 0001 0100 | 1001 | |
| 15 | 1111 | F | 17 | 0001 0101 | 1000 |
Hexadecimal para la conversión decimal
El ejemplo siguiente permite comprender cómo realizar la conversión hexadecimal a decimal
Ejemplo: Convertir el número hexadecimal (5 F)16 a su valor decimal equivalente
El número hexadecimal (5 F)16 puede escribirse como sigue
= 5 x 162 + A x 161 + F x 160
Reemplazar los números hexadecimales por sus valores decimales equivalentes y realizar la operación aritmética
A = 10 and F = 15;
= 5 x 162 + 10 x 161 + 15 x 160
= 1280 + 160 + 15 = 1455
El equivalente decimal es (1455)10
Conversión de decimal a hexadecimal
Ejemplo: Convertir el número hexadecimal (5 F)16 a su valor decimal equivalente
El número hexadecimal (5 F)16 puede escribirse como sigue
= 5 x 162 + A x 161 + F x 160
Reemplazar los números hexadecimales por sus valores decimales equivalentes y realizar la operación aritmética
A = 10 and F = 15;
= 5 x 162 + 10 x 161 + 15 x 160
= 1280 + 160 + 15 = 1455
El equivalente decimal es (1455)10
Conversión de decimal a hexadecimal
Decimal a hexadecimal conversión puede lograrse por método de división sucesivas. En el siguiente ejemplo permite comprender cómo realizar decimal a hexadecimal conversión
Ejemplo: Convertir el número decimal 2250 a su equivalente hexadecimal
http://es.ncalculators.com/digital-computation/hex-decimal-converter.htm
- Realizado por: Valeria Rojas Orduz Grado 9A Colegio Integrado Nuestra Señora del Divino Amor



Comentarios
Publicar un comentario